AND 연산에는 두개의 input 과 하나의 ouput 이 있습니다. input 을 $x_{1}$ 과 $x_{2}$ 라고 놓고, ouput 을 $\hat{y}$ 라고 놓겠습니다. AND 연산의 규칙을 표로 나타내면 아래와 같습니다.

AND 연산은 참을 1, 거짓을 0이라고 두었을 때, 두 input 값이 모두 참일 때만 ouput 이 참이 됩니다.
AND 연산을 수행하는 신경망을 만들어봅시다. input 의 종류가 두개이고 ouput 이 하나인 신경망의 형태는 아래와 같습니다. 가장 단순한 형태인 단층퍼셉트론입니다. 입력층과 출력층으로만 구성되어 있습니다. 입력층은 층 수로 세지 않기 때문에 단층퍼셉트론 이라고 부릅니다. 가장 왼쪽의 x 들이 입력층이고, 가운데 살색 층이 출력층입니다.
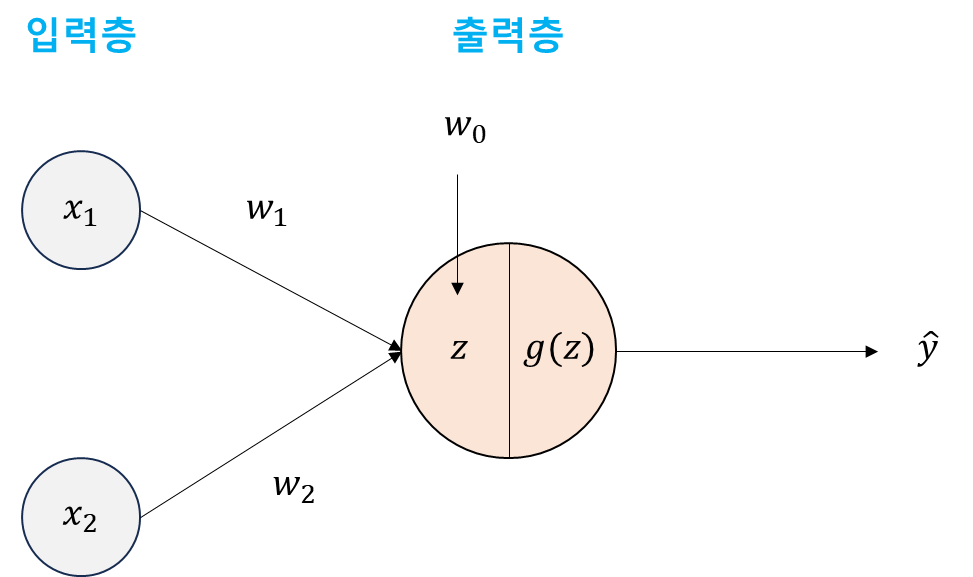
위 신경망 그림은 아래와 같은 형태로도 쓸 수 있습니다.
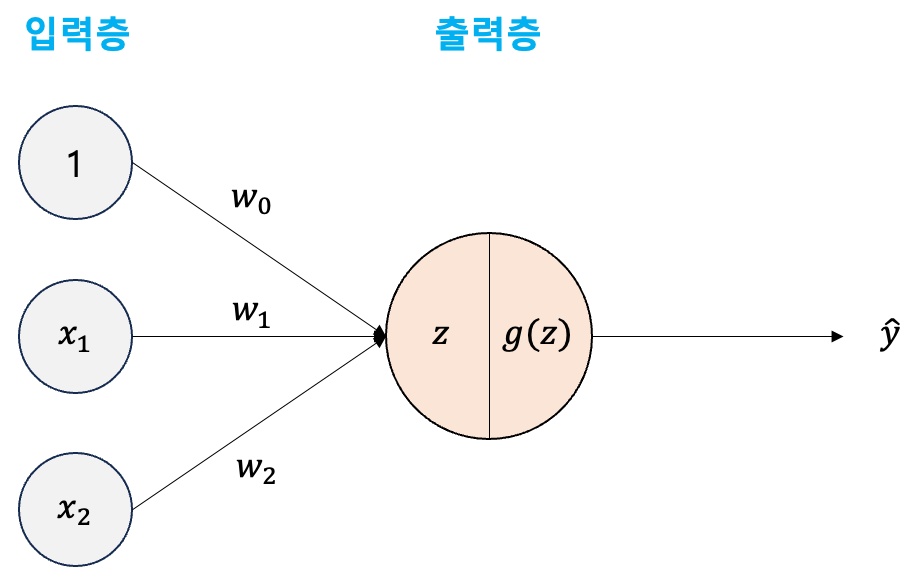
z는 아래와 같이 계산됩니다.
$z=w_{0}+w_{1}x_{1}+w_{2}x_{2}$
z를 계산하는 함수를 전달함수(transfer function)이라고 부릅니다. 위 식에서 $w_{0}$는 일차함수의 상수 역할을 한다는 것을 알 수 있습니다. $w_{0}$는 bias(편향)라고 부릅니다. 2차원 공간에서 bias는 직선의 상하 위치를 결정하는 역할을 합니다. 직선의 상하 위치를 결정하는 bias가 왜 필요한지는 뒷부분에 가면 알 수 있습니다.
위 식을 더 간단한 형태로 나타내기 위해 아래와 같은 벡터를 정의하겠습니다.
$\vec{x}=\begin{bmatrix}
1\\
x_{1}\\
x_{2}
\end{bmatrix}$
$\vec{w}=\begin{bmatrix}
w_{0}\\
w_{1}\\
w_{2}
\end{bmatrix}$
z는 아래와 같이 나타낼 수 있습니다.
$z=w^{T}x$
이제 z를 g(z) 안에 넣어 값을 구해야 합니다. g(z)는 활성화 함수(activation function)입니다. 활성화 함수는 우리가 정하면 됩니다. 뒤에서 정하겠습니다.
우리는 AND 신경망을 만들고 있습니다. $w_{0}$, $w_{1}$, $w_{2}$ 를 적절히 설정해서 AND 연산을 수행하는 신경망을 만들 것입니다.
AND 연산 표를 그래프로 그려보면 아래와 같습니다. y값이 0인 경우를 빨간색, 1인 경우를 초록색으로 그렸습니다.

위 그림을 잘 보면 직선을 이용하여 $\hat{y}$ 을 나누는 기준을 삼을 수 있다는 것을 알 수 있습니다. 직선을 아래와 같이 그리면 됩니다.
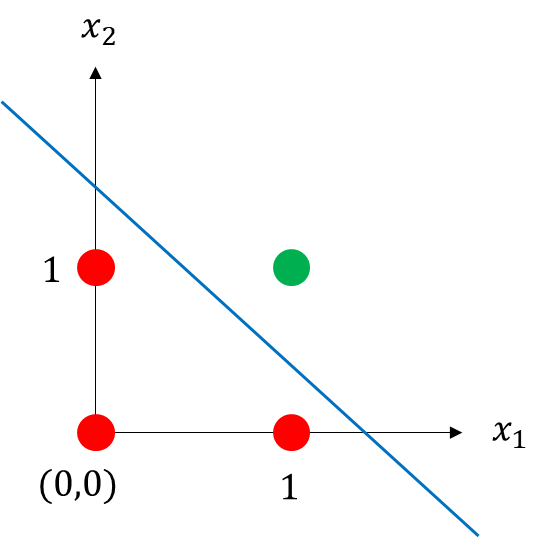
여러 직선이 가능한데 $(1.5,0)$ 과 $(0,1.5)$를 지나는 직선으로 정하겠습니다. 이 직선의 방정식은 아래와 같습니다.
$x_{2}=1.5-x_{1}$
아래와 같이 정리하겠습니다.
$-1.5+x_{1}+x_{2}$
(1,1) 을 넣어보면 위 값은 양수가 됩니다. (1,1) 은 $\hat{y}$이 1인 곳입니다. 위 식을 z로 정의합시다.
$z=-1.5+x_{1}+x_{2}$
따라서 $w_{0}$은 -1.5, $w_{1}$ 과 $w_{2}$ 는 1입니다.
이제 활성함수 $g(z)$를 정의해야 합니다. z가 0보다 크면 $\hat{y}$이 1이고, 0보다 작으면 $\hat{y}$ 이 0이 되도록 활성함수를 정의하면 됩니다. 활성함수를 아래와 같이 정의할 수 있습니다.
$g(z)=\left\{\begin{matrix}
z>0 & 1\\
z<0 & 0
\end{matrix}\right.$
완성된 신경망은 아래와 같습니다.

파이썬으로 구현하면 아래와 같습니다.
x1=1
x2=0
z=-1.5+x1+x2
if z>0 :
y=1
elif z<0 :
y=0
print(y)'머신러닝 이론 (딥러닝) > 손으로 푸는 딥너링(지움)' 카테고리의 다른 글
| [손으로 푸는 딥러닝] 6. XOR 신경망 수식 세우기 (0) | 2023.10.16 |
|---|---|
| [손으로 푸는 딥러닝] 5. XOR 연산 신경망으로 구현하기 (0) | 2023.10.16 |
| [손으로 푸는 딥러닝] 4. 단층퍼셉트론의 수학적 이해 (0) | 2023.10.12 |
| [손으로 푸는 딥러닝] 3. OR 연산 신경망으로 구현하기 (0) | 2023.10.10 |




댓글