[파이썬] 사인함수 예측 예제 (gradient decent)

gradient decent 를 이용하여 사인함수를 예측하는 예제입니다. 설명은 주석으로 대신합니다. 

 

import math
import torch
import matplotlib.pyplot as plt

#data생성
x=torch.linspace(-math.pi,math.pi,1000)
y=torch.sin(x)

#weight 초기화
w0=torch.randn(())
w1=torch.randn(())
w2=torch.randn(())
w3=torch.randn(())

learning_rate=1e-6
MSE_list=[]

#gradient decent 적용
for epoch in range(30):

	#예측 함수 설정
    y_pred=w3*x**3+w2*x**2+w1*x+w0

    #loss
    MSE=(y_pred-y).pow(2).sum().item() 
	
    #gradient 계산
    grad_w3=(2*(y_pred-y)*x**3).sum()
    grad_w2=(2*(y_pred-y)*x**2).sum()
    grad_w1=(2*(y_pred-y)*x).sum()
    grad_w0=(2*(y_pred-y)).sum()

    #update
    w3 = w3-learning_rate*grad_w3
    w2 = w3-learning_rate*grad_w2
    w1 = w3-learning_rate*grad_w1
    w0 = w3-learning_rate*grad_w0

    MSE_list.append(MSE)
    print(f"epoch{epoch+1} loss:{MSE}")


#MSE 를 그래프로
fig, ax = plt.subplots(1,1)
ax.plot(MSE_list, label='MSE',linestyle='solid',marker='')
#ax.legend()
ax.set_title('MSE')
ax.set_xlabel('epoch')
ax.set_ylabel('MSE')
plt.show()

 

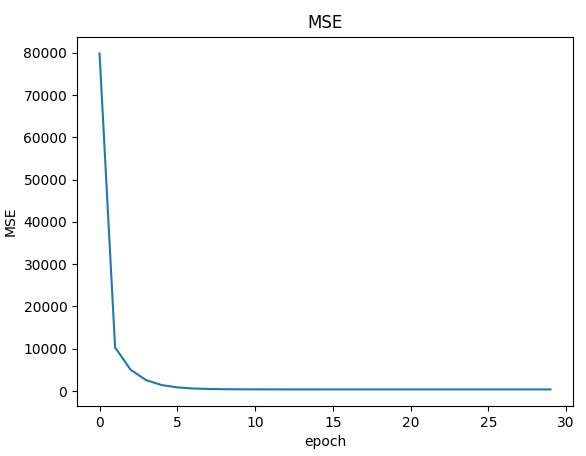
아래는 출력 그래프입니다. 오차값을 나타냅니다.