KL divergence 는 아래와 같이 정의됩니다.
$D_{KL}(p||q)=H[p,q]-H[p]$
크로스엔트로피와 엔트로피의 차이입니다. 수식을 자세히 쓰면 아래와 같습니다.
$D_{KL}(p||q)=\int_{-\infty}^{\infty}p(x)\ln \frac{p(x)}{q(x)}dx$
이번 시간에는 KL divergence가 항상 양수라는 것을 증명하겠습니다. 증명에는 아래 부등식이 사용됩니다.
$\ln x \leq x-1$ $(x>0)$
위 부등식을 먼저 증명하겠습니다. 위 식을 아래와 같이 변형합니다.
$x \leq e^{x-1}$
아래와 같이 이항합니다.
$0\leq e^{x-1}-x$
우변의 식을 f(x)라고 놓겠습니다 f(x)가 x가 양수인 영역에서 항상 0보다 크다는 것을 증명하면 됩니다. f(x)를 미분하여 개형을 파악해봅시다. f(x)의 미분은 아래와 같습니다.
$f'(x)=e^{a-1}-1$
그래프는 아래와 같습니다.
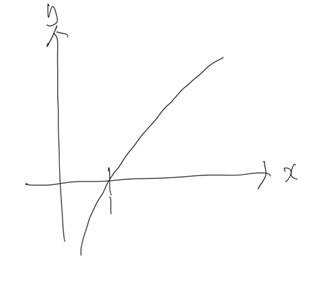
따라서 f(x)의 그래프 개형은 x=1 까지 감소했다가 다시 증가하는 형태입니다. f(1) 은 0이므로 f(x)는 항상 0보다 큽니다. 우리는 지금까지 아래 부등식을 증명했습니다.
$\ln x \leq x-1$ $(x>0)$
본격적으로 KL divergence 가 0보다 크다는 것을 증명해봅시다. 아래 식에서 출발합니다.
$D_{KL}(p||q)=\int_{-\infty}^{\infty}p(x)\ln \frac{p(x)}{q(x)}dx$
우변을 아래와 같이 변형합시다. 마이너스를 붙이고 로그 진수의 분자와 분모를 바꿔주었습니다.
$D_{KL}(p||q)=-\int_{-\infty}^{\infty}p(x)\ln \frac{q(x)}{p(x)}dx$
양변에 마이너스를 곱해줍니다.
$-D_{KL}(p||q)=\int_{-\infty}^{\infty}p(x)\ln \frac{q(x)}{p(x)}dx$
우변에 우리가 유도한 부등식을 적용합시다.
$-D_{KL}(p||q)=\int_{-\infty}^{\infty}p(x)\ln \frac{q(x)}{p(x)}dx\leq \int_{-\infty}^{\infty}p(x)\left ( \frac{q(x)}{p(x)}-1 \right )dx$
맨 오른쪽 변을 아래와 같이 변형합니다.
$-D_{KL}(p||q)=\int_{-\infty}^{\infty}p(x)\ln \frac{q(x)}{p(x)}dx\leq \int_{-\infty}^{\infty}\left (q(x)-p(x) \right )dx$
맨 오른쪽 변의 미분을 아래와 같이 분리해서 써줍니다.
$-D_{KL}(p||q)=\int_{-\infty}^{\infty}p(x)\ln \frac{q(x)}{p(x)}dx\leq \int_{-\infty}^{\infty}q(x)dx-\int_{-\infty}^{\infty}p(x)dx$
확률분포의 합은 1이므로 맨 오른쪽 변은 0이 됩니다.
$-D_{KL}(p||q)=\int_{-\infty}^{\infty}p(x)\ln \frac{q(x)}{p(x)}dx\leq 0$
따라서 아래 부등식이 유도됩니다.
$D_{KL}(p||q)\geq 0$
'기타 강의 > KL divergence 의 이해' 카테고리의 다른 글
| [KL divergence 의 이해] 7. ELBO 도 무엇인지 알아보자 (0) | 2023.10.25 |
|---|---|
| [KL divergence 의 이해] 6. 그냥 크로스 엔트로피를 쓰면 되는 이유 (0) | 2023.10.06 |
| [KL divergence 의 이해] 4. 크로스 엔트로피와 KL divergence (0) | 2023.10.05 |
| [KL divergence 의 이해] 3. 엔트로피가 높은 확률분포란? (0) | 2023.10.05 |
| [KL divergence 의 이해] 2. 엔트로피 (확률분포의 정보량) (0) | 2023.10.05 |
댓글